3º CASO: SACAR DECIMALES EN DIVISIONES QUE NO SON EXACTAS

Las divisiones no son exactas cuando el resto no es cero. En ese caso, el resultado se indica diciendo un número natural y el resto.

Por ejemplo:

La primera cifra del dividendo es más pequeña que el divisor, por tanto empezamos cogiendo 2 cifras del dividendo, es decir, dividimos 25 entre 6. El número que multiplicado por el divisor es más pequeño que 25 es el 4:

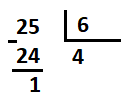
El resto es más pequeño que el cociente y hemos terminado de dividir.

Por tanto el resultado de dividir 25 entre 6 es 4 y me sobra 1 (o de resto 1). Hemos expresado el resultado indicando el cociente y el resto.

Sin embargo, en este caso, que el resultado no es exacto, podemos expresar el resultado también con decimales, es decir, un número que tendrá una parte entera y una parte decimal.

Vamos a ver cómo hacerlo, con el mismo ejemplo de antes:

Nos quedamos en que el cociente era 4 y teníamos de resto 1:

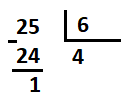
Hemos terminado de dividir todas las cifras enteras, por lo que a partir de ahora, empezamos a obtener la parte decimal del resultado. Para seguir, bajamos un cero y añadimos una coma en el cociente:

Ahora seguimos dividiendo 10 entre 6. El número que multiplicado a 6 es menor que 10 es el 1, que nos da de resto 4. Este 1 ya forma parte de la parte decimal del resultado:

El resto que nos ha quedado sigue siendo menor que 6, por tanto para seguir dividiendo, bajamos otro cero: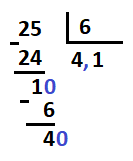

Seguimos dividiendo 40 entre 6. El número que multiplicado a 6 es menor que 40 es el 6, que nos da de resto 4. Este 6 es otra cifra de la parte decimal del cociente:

En este caso, podríamos seguir así de forma  infinita, porque siempre tendríamos de resto 4. Tenemos un decimal periódico mixto